Quotient Rule (몫 규칙 = 나눗셈의 미분)

<< 미적분학에서 두 함수의 나눗셈의 도함수를 구하는 규칙입니다.  >>

 

몫 규칙

 

 

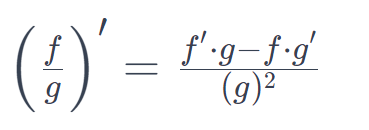
1.설명

• 각 함수의 도함수를 개별적으로 구한 다음 공식에 대입하여 계산할 수 있습니다.

2. 증명

이해를 쉽게하자면 f'(x)  계산 과정 3번째 줄에 각 분모에 -h(x)g(x)를 하는 것을 곰곰히 생각하시면 공식 증명은 쉽습니다.

Quotient Rule 증명

 

3. 활용 (기초)

예제1

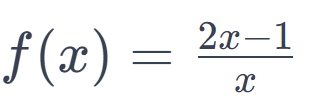
위의 미분을 구하시오.

g(x) = 2x-1

h(x) = x  라고 할 때.

도함수 먼저 계산하면,

g'(x) = 2

h'(x) = 1

 

따라서, ( 2x  -  (2x-1) )  /   x^2 가 됩니다.

 

이를 계산하면, 최종 도함수는 1 /x^2   로 표현됩니다.

 

 

 

3. 활용 (심화)

chain Rule 과 Quotient Rule , Power Rule 과 같이 함께 사용하면 환상의 하모니가 열립니다. ~~~

아래의 문제를 풀어보세요

예제2

chain Rule 을 이용합니다.

5( (t-4) / (t-1) )^4   * d/dt ( (t-4)  / t-1)  )

 

Quotient Rule 을 이용합니다.

5( (t-4) / (t-1) )^4   * ( t-1 - t-4)  / (t - 1)^2

 

=> 5( (t-4) / (t-1) )^4   *  (-5  /  (t - 1)^2)

 

=>  -25 (t-4)^4   /  (t - 1 )^6

 

https://knowledge-skills.tistory.com/52

Chain Rule (연쇄 법칙)