exponential Function (지수 함수)

<< 일반적으로 밑이 상수이고 지수가 변수인 함수 >>

 

지수 함수

 

1.설명

• 지수(x)는 실수 값을 가지는 변수가 됩니다.
• 밑(a)는 양의 상수 입니다.

※  여기서 밑(a) 가 음수인 경우도 성립은 된다. 이는 다음 글에서 설명 하겠습니다. (feat, 오일러 공식)

2. 특징 

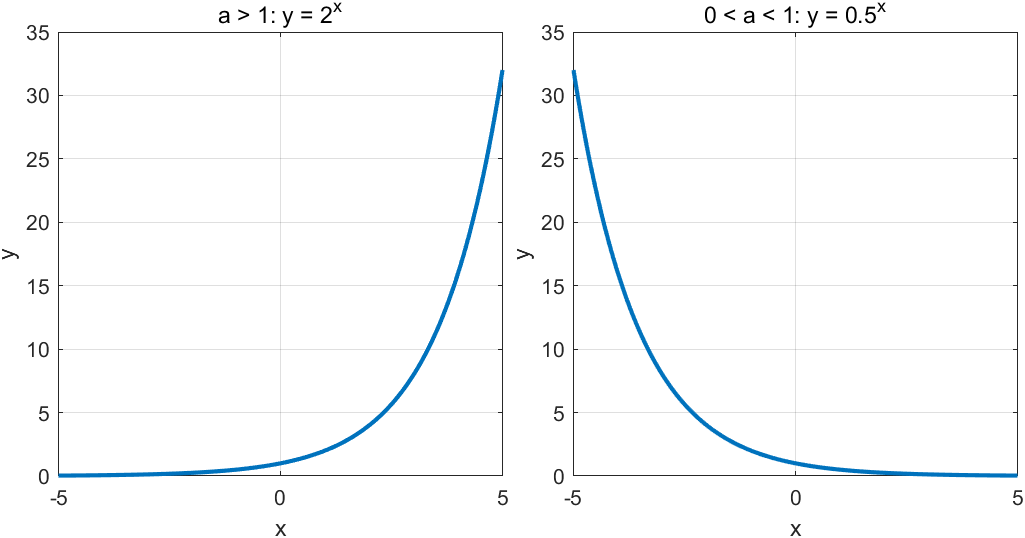
1. a > 1인 경우 : x가 증가함에 따라 무한히 커지고, x가 감소함에 따라 무한히 작아집니다
2. 0 < a < 1인 경우 : x가 증가함에 따라 0으로 수렴하고, x가 감소함에 따라 무한히 커집니다.
3. a = 1인 경우: 지수 함수는 상수 함수로 변합니다. 즉, 모든 x에 대해 값이 1로 일정합니다.
4. 음수 지수의 경우: 지수 함수에서 음수 지수는 분수로 표현될 수 있습니다. 예를 들어, a^-x =1/a^x아래의 그래프를 참고하면 이해를 쉽게 할 수 있습니다.

좌( 1) , 우 (2)

좌(3) , 우(4)